您知道相似三角形的判定方法有哪些呢?
来源:51EDU精品学习网 编辑:sx_wangha
2018-09-14 11:13:23
在解相似三角形的判定方法有很多,您知道有哪些方法吗?以下是我们为大家搜集整理的相似三角形的判定方法,希望可以帮到大家~
相似三角形的判定方法
由于从定义出发判断两个三角形是否相似,需考虑6个元素,即三组对应角是否分别相等,三组对应边是否分别成比例,显然比较麻烦。所以我们曾经给出过如下几个判定两个三角形相似的简单方法:
(1)如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似;
(2)如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似;
(3)如果一个三角形的两个角和另一个三角形两个角对应相等,那么这两个三角形相似。
相似三角形的判定习题及答案
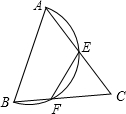
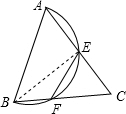
1、如图,在锐角△ABC中,以AB为直径的半圆分别交AC、BC于E、F,且△CEF∽△CBA,若S△CEF=1/4 S△ABC,则∠C=______.
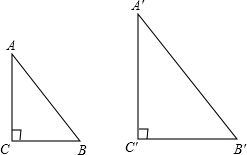
2、如果Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,AB=3,BC=2,A′B′=12,则A′C′=______.
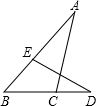
3、已知在△ABC中,AB=20,AC=12,BC=16,点D是射线BC上的一点(不与端点B重合),连接AD,如果△ACD与△ABC相似,那么BD=______.
4、如图,已知△ABC∽△DBE,AB=8,DB=6,则S△ABC:S△DBE=______.
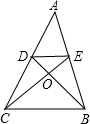
5、如图,△OED∽△OCB,且OE=6,EC=21,则△OCB与△OED的相似比是( )
A.3/7 B.5/2 C.8/5 D.3/5
相似三角形的判定答案
1、∵△CEF∽△CBA,S△CEF=1/4
S△ABC,
∴CE/CB=1/2,
连接BE,
∵AB是直径,
∴∠BEA=90°,
∴∠BEC=180°-90°=90°,
∴cosC=CE/CB=1/2,
∴∠C=60°,
故答案为:60°.
2、首先根据勾股定理及已知条件AB=3,BC=2,求出AC=√32-22=5,
因为Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,且A′B′=12,
则Rt△ABC与Rt△A′B′C′的相似比是1:4,
所以A′C′=4AC=4√ˉ5
3、①若点D在线段BC上,
∵△ACD∽△ABC,
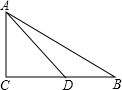
∴
ACBC=CDAC,即1216=CD12,
解得:CD=9,
则BD=BC-CD=16-9=7;
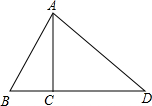
②若点D在线段BC的延长线上当△ACD∽△ABC时,则ACBC=CDAC,即1216=CD12,
解得:CD=9,
则BD=BC+CD=16+9=25;
当△ACD∽△ACB时,则ACAC=CDBC,即1216=12CD,
∴CD=16,
则BD=BC+CD=16+16=32.
故答案为:7或25或32.
4、∵△ABC∽△DBE,AB=8,DB=6
∴S△ABC:S△DBE=(ABDB)2=(86)2=16:9.
5、∵△OED∽△OCB,
∴△OCB与△OED的相似比即为OC与OE的比值,
又OE=6,EC=21,
∴OC:OE=(21-6):6=15:6=5:2,
故选B.
相似三角形的判定方法您学会了吗?我们还为大家整理了锐角三角形考点归纳、相似三角形重要考点 、三角形的三边关系知识点 ,希望可以帮到大家~
- 2019-03-06 17:09:27
- 2019-03-06 16:09:00
- 2019-03-06 15:08:03
- 2019-03-06 14:26:30
- 2019-03-06 13:23:04
- 2019-03-06 11:13:55
- 2019-03-06 10:07:29
- 2019-03-06 09:38:58
- 2019-03-04 16:18:37
- 2019-03-04 15:15:23
免责声明
精品学习网(51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。
- [原创]初一数学下册思维导图:整式的乘...
- [原创]初一数学下册思维导图:相交线与...
- [原创]初一数学下册思维导图:三角形知识点
- [原创]初一数学思维导图:变量之间的关...
- [原创]初一数学下册思维导图:生活中的...
- [原创]初一数学下册知识点:概率初步
- [原创]初一数学知识点:代数初步知识点
- [原创]初一数学知识点:有理数知识点
- [原创]初二政治:丰富的社会生活知识点
- [原创]人教版初二政治:网络生活新空间...